3D

RUANG
    3 DIMENSI 三维

3 dimension

Seperti apa yang dikatakan sebelum ini, ruang 3 dimensi merupakan ruang yang paling mudah difahami kerana kita hidup dalam dunia yang dicipta dalam ruang 3 dimensi.
就如之前所说的一样，三维空间是所有空间中最容易明白的因为我们正活在三维的空间中。
As mentioned earlier, 3-dimensional space is the easiest space to understand as we live in a world created in 3-dimensional space.

Contoh-contoh bagi ruang 3 dimensi ialah:
三维空间的例子有：

Examples of 3 dimension shape are :

Gambar Rajah 图片 Picture	Nama 名称 Name	Bucu 角 Vertices	Sisi 边 Sides	Permukaan 平面 Surface
	Kiub / Kubus 正方体 Cube	8	12	6
	Kuboid 长方体 Cuboid	8	12	6
	Sfera 球体 Sphere	0	0	1
	Piramid 角锥体 Pyramid	5	8	5
	Kon 圆锥体 Cone	1	1	2
	Silinder 圆柱体 Sylinder	0	2	3

Melalui jadual di atas, dapatlah kita perhatikan perbezaan bilangan bucu, sisi dan permukaan antara beberapa bentuk yang telah dinyatakan.
通过上表，我们可以观察到每个形状在角的数量，边的数量和平面数量上的差别。
Based the table, we can observe the difference on nombor of vertices, sides and surfaces of every 3D-shape.

Seterusnya, marilah kita menelitikan cara-cara untuk mengira isipadu, iaitu ruang yang diisi bagi bentuk- bentuk 3 dimensi,
接下来， 让我们一起来研究计算形状的体积，也就形状所占用的空间的方式。
Then, let us study the ways to calculate volume ( space occupied ) of each 3D-shape.

Pertama sekali, Kiub dan Kuboid,
第一个是正方体和长方体,
First of all, cube and cuboid,

Kiub dan Kuboid mempunyai bilangan bucu, sisi dan permukaan yang sama. Oleh itu, cara pengiraan isipadu mereka adalah serupa, iaitu :
正方体和长方体拥有相同数量的角，边和平面。因此，它们体积的计算方式时相似的，也就是：
Cube and cuboid had the same nombor of vertices, sides and surfaces. So, they have the similar way to calculate their volume :

Isipadu

=Keluasan tapak x Tinggi

= Panjang x Lebar x Tinggi

体积
= 底部面积 x 高
= 长 x 宽 x 高

Volume
= Base area x Height
= Long x Width

Namun, kita haruslah memberikan perhatian kepada bentuk kiub yang mempunyai semua sisi yang sama panjang, oleh itu, formula isipadu kiub juga boleh didefinisikan sebagai :

尽管如此，我们仍应该对正方体的体积的计算方式给予关注，因为正方体拥有同等长的边。因此，我们也可以这样计算正方体的体积：
Anyway, we still have to pay attention on the way to calculate volume of cube which has the same long sides. So, the way to calculate volume of cube also can be defined as :

Panjang x Panjang x Panjang

长 x 长 x 长
Long x Long x Long

Sfera,
球体，
Sphere,

Bentuk Sfera tidak mempunya tapak yang rata, sebaliknya sfera hanya mempunyai satu permukaan yang melengkung dan bulat, oleh itu, nilai π perlu dimasukkan dalam formula pengiraan isipadu sfera :
球体没有一个平面的底部，相反的，球体只拥有一个有弧度的圆面。因此，计算球体体积的方程式里需应用到π：
Sphere doesnt have a flat surface, vise versa, it only have a curved suface. Thus, we should involve π in it's calculation of volume :

Isipadu
体积
Volume
=(4/3)πr^3

di mana r mewakili jejari sfera.
r 代表球体的半径
r represent radius of sphere.

Piramid dan Kon,
角锥体和圆锥体,
Pyramid and cone,

Piramid dan kon mempunyai satu tapak rata dan satu atau lebih daripada satu permukaan menegak, oleh itu, isipadu piramid dan kon boleh dirumuskan seperti berikut :
角锥体和圆锥体都拥有一个平面底部和一个或超过一个直角平面。因此，角锥体和圆锥体的体积可以如此计算：
Pyramid and cone both have one flat base and one or more than one right-angle aurface. Thus, volume formula of pyramid and cone can be defined as :

Isipadu

=(1/3) x Keluasan tapak x Tinggi

体积
= （1/3） x 底部面积 x 高

Volume
= (1/3) x Base area x Height

Mengapakah kita harus mendarabkan luas tapak dan tinggi piramid dan kon dengan (1/3)? Hal ini kerana isipadu piramid merupakan (1/3) daripada kuboid yang mempunyai luas tapak yang sama, manakala isipadu kon merupakan (1/3) daripada silinder yang mempunyai luas tapak sama.
为什么我们需要把角锥体和圆锥体的底部面积乘与其直角高度之后再乘与三分之一？这是因为角锥体的体积是与和它拥有同等底部面积的长方体的体积三分之一，而圆锥体的体积则是与和它拥有相同底部面积的圆柱体的体积的三分之一。
Why we should multiply the area of base and height of the pyramid and cone with (1/3)? This is because volume of pyramid is (1/3) of cuboid which has the same base area, while volume of cone is (1/3) of cylinder which has the same base area.

Silinder,
圆柱体，
Cylinder,

Bentuk silinder mempunyai satu tapak bulat yang rata, oleh itu cara pengiraan isipadunya juga haruslah melibatkan nilai π seperti cara pengiraan isipadu sfera. Iaitu :
圆柱体拥有一个圆形的平面底部，因此圆柱体的体积的计算方式应该加入π，就如球体体积的计算方式一样。那就是：
 cylinder has a round base, thus, it's formula of volume should include π :

Isipadu
=Keluasan tapak x Tinggi
= πr² x Tinggi

体积
= 底部面积 x 高
= πr² x 高

Volume
= Base area x Height

Selain itu, kita juga boleh mengira jumlah luas permukaan bagi jaring setiap bentuk 3 dimensi dengan menjumlahkan luas permukaan mereka.
除此之外，我们也可以通过加上每个形状各自的面积的总数来得出它们的总面积。
Besides, we also can calculate the total surface area of every 3D-shape  by total up their surface area.

Contohnya :
比方说：
For an example : 

Kubus
正方体
Cube

 
Jumlah luas permukaan
= sisi x sisi x 6

总面积
= 边 x 边 x 6

Total surface area
= side x side x 6

Kuboid
长方体
Cuboid









Jumlah luas permukaan

= ( luas tapak x 2) + ( luas permukaan hadapan x 2 ) + ( luas permukaan bahagian tepi x 2 )

总面积
= （底部面积 x 2）+（前面面积 x 2）+（侧面面积 x 2）

Total surface area
= (Base area x 2) + (Front area x 2) + (Side area x 2)


Piramid
角锥体
Pyramid



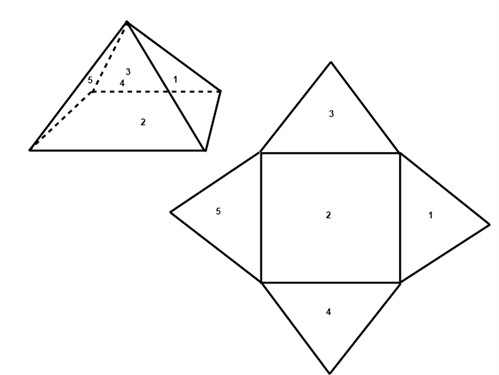
Jumlah luas permukaan
= luas permukaan tapak + ( luas permukaan segi tiga x 4 )

总面积
= 底部面积+（三角形面积 x 4）

Total surface area
= Base surface + (Triangle area x 4)


Silinder
圆柱体
Cylinder


Jumlah luas permukaan
= ( luas tapak x 2 ) + ( luas segi empat )
= 2πr^2 + 2πrh

总面积
=（底部面积 x 2）+（四边形面积）
= 2πr^2 + 2πrh

Total surface area
= (Base area x 2) + （Area of  rectangle）



Kon
圆锥体
Cone

Luas permukaan
= πr² x πlr
di mana r mewakili jejari tapak kon yang berbentuk bulatan dan l mewakili ketinggian sisi sendeng.

总面积
= πr² x πlr
r 代表底部半径，l 代表斜面高度。

Total surface area
= πr² x πlr
r represent radius  of round base of cone while l represent height of the side of cone.



Sfera
球体
Sphere

Luas permukaan
= 4πr<sup>2

总面积
=</sup> 4πr²

Total surface area
= 4πr²